Eficiência x Eficácia x Efetividade

Prezadas e prezados, não é incomum eu entrar em certos embates com discentes para argumentar quanto a validade ou não de uma solução para um problema. Numa ocorrência recente, a solução proposta resolvia o problema, mas não usar as ferramentas adequadas para tal. Procurei argumentar, mas a réplica sempre vem de forma contundente: “Mas está funcionando! Resolve o problema!”.

Para argumentar de uma maneira mais clara, resolvi desenhar! :D Para tal, uso 3 conceitos vistos em cursos de administração e afins, mas que estão em nosso entorno o tempo todo: eficiência, eficácia e efetividade. Para os desatentos, podem entender que se trata da mesma coisa, mas não é bem assim. Falando de forma bem direta e sucinta, eficiência analisa quão bons são os métodos escolhidos para se resolver um problema, eficácia analisa se o problema está sendo resolvido de fato, independente de como, e efetividade analisa se a resolução do problema está de fato atendendo da forma que se esperava.

Eu criei um diagrama abaixo e acho que deturpei um pouco o significado de efetividade, pois a coloquei como uma interseção de eficiência e eficácia. Entretanto, isso atende muito bem à minha argumentação junto aos estudantes.

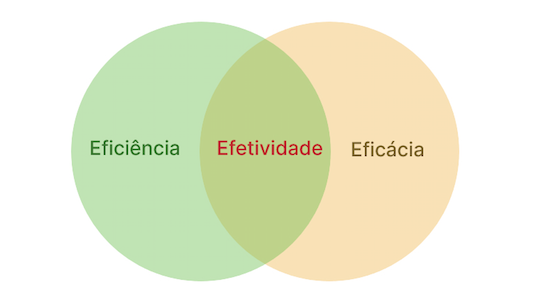
(Abrindo um parênteses, o diagrama acima é um Diagrama de Venn , ferramenta muito útil e utilizado, dentre outras coisas, na ilustração de conjuntos na BOAtemática. Segue um site interessante para a criação desses diagramas. Fecha parênteses).

Considere que queiramos calcula o n-ésimo termo da série de Fibonacci . (Os códigos abaixo são fornecidos na linguagem LUA , a única linguagem de programação “codada” no mundo e que foi desenvolvida abaixo da linha do Equador, por um grupo na PUC-Rio).

function fib(n)
  if (n == 1) then return 1 
  elseif (n == 2) then return 1 
  else return fib(n-1) + fib(n-2)
  end
end
print(fib(10))

O código acima funciona. Entretanto, há uma recursão dupla na chamada que cria redundância e torna o desempenho desse programa proibitivo para números maiores (acima de 40 já começa a ficar bem ruim a execução em qualquer linguagem que rodemos). Este seria um exemplo de código eficaz. Ele resolve o problema, mas não de uma forma “interessante”, para não entregar a ideia do código seguinte.

Agora veremos uma forma diferente, muito pouco difundida, pois não desafia tanto do ponto de vista de programação.

function fib(n)
  fi = 1.618034
  return (fi ^ n) / math.sqrt(5)
end
print(fib(10))

O código anterior é uma forma aproximada, e ultraeficiente, de se chegar a um elemento da série de Fibonacci. Observe que a função apenas retorna o resultado de uma expressão, sem muito esforço computacional, exceto para o cálculo do expoente e da raíz quadrada. Ele se baseia na Fórmula de Binet .

Entretanto, se queremos uma forma efetiva (na minha interpretação) de resolução deste problema, ou seja, que seja eficiente, ágil, e resolva o problema de forma eficaz, podemos fazer a implementação iterativa abaixo, que não é nada custosa, se comparada a primeira versão, e é exata, se comparamos à segunda versão.

function fib(n)
  ant = 1
  prox = 1
  while (n > 1) do
    ant, prox = prox, ant+prox
    n = n-1
  end
  return ant
end
print(fib(10))

Resumindo, quando pedimos a resolução de problemas num ambiente de aprendizagem, sempre esperamos por soluções efetivas. Soluções eficientes e eficazes são interessantes para se explorar as diferentes possibilidades de resolução, mas não devemos nos contentar com elas! ;)